Answer:
First we need to analyse each mass and all the forces that interact with each of them. To do that, we use a free-body diagram and from that it'll be easier to analyse all the forces and write the mathematical relation between them, each free-body diagram is attached.
From these diagrams and using Newton's Law
 , we define a equation for each mass.
, we define a equation for each mass.
Mass 1:
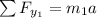
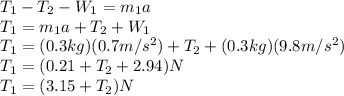
Now, we need to find a expression for the second tension and solve the equation.
Mass 2:
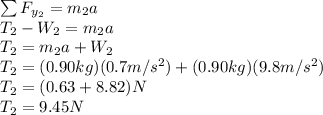
Now, we replace the second tension in the first equation:
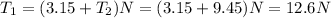
Therefore, with an upward acceleration, the tensions are
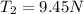 and
and
 .
.
On the other hand, we downwards acceleration, we just need to change 0.7 by -0.7, and then solve.
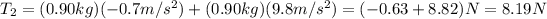 .
.
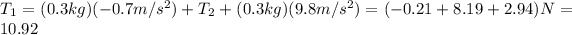 .
.
Therefore, with downwards acceleration, tensions would be
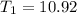 and
and
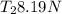 .
.