Question

If a positively charged particle moves into a magnetic field traveling in a straight line, how would you expect its motion to change?

Answer 1

Charged particles traveling in a magnetic field undergo something called the Lorentz Force, which is given by:

`F=q(v * B)`
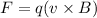
where q is the charge, v is the velocity vector, and B is the magnetic field (technically it's the magnetic flux density, a scaled version of the magnetic field)
This equation means the force on the particle is perpendicular to the magnetic field and velocity vectors. If the particle travels perpendicular to the field initially, then the particle will travel in a circle. This is because as the velocity changes (the particle curves a little due to the force) a new force occurs that is now perpendicular to the new velocity, causing it to curve more, and so on. The radius of curvature of a particle traveling in a magnetic field that is always perpendicular to the instantaneous velocity is found by setting the radial force equal to the simplified form of the Lorentz force, F=qvB (we can simplify it by dropping the cross product since we are saying the velocity is perpendicular and so it becomes a standard product of magnitudes of the vectors):
The radial force of a particle traveling in a circle is

`F_(rad)= (mv^2)/(r)`
So we get

`(mv^2)/(r) =qvB \\ \\ then \\ \\ r= (mv)/(qB)`
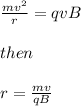
Which is known as the Larmor radius