Question

What is the area of this figure?



Enter your answer in the box.
units²

Answer 1

`42`
`units^2`

Explanation:

A simpler and faster way of solving this problem is through Pick's Theorem.

The theorem states that the area of any given shape (Specifically polygons) on a grid is the number of internal points (every point inside the shape) added to the quantity of the number of boundary points (Every point that is exactly on a point of the grid and is a part of the perimeter of the shape) divided by 2. Take this quantity and subtract 1 and it shows like so,

`A=I+(B)/(2)-1`.

In this case, we see that there are 36 internal points and 14 boundary points. So in turn, we get

`A=36 + (14)/(2)-1\\A=36+7-1\\A=43-1\\A=\boxed{42}`

Hence giving our desired result of 42 square units.

Answer 2

Given is the irregular hexagon.

We can divide the given figure into two triangles and one rectangle, and then find areas of each, and then add all of them to find the final answer.

We can find the dimensions by counting the blocks on graph. Given two triangles are identical in shape with base (b=7) and height (h=2).

The area of triangle
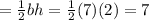`=(1)/(2) bh = (1)/(2) (7)(2) = 7` squared units.

Area of two triangles = 14 squared units.

Rectangle has length (l) same as base (b) of triangle i.e. l=7 and width (w=4).

Area of rectangle = l × w = 7 × 4 = 28 squared units.

Total area = 14 + 28 = 42 squared units.

So, final answer is 42 squared units.