Question

What is the solution of 3+ (x-2)/(x-3) <=4

X<3
X<=3
X>3
X>=3

Answer 1

I believe that it's x<3

Answer 2

A. X < 3.

Explanation:

We have the equation,
`3 + (x-2)/(x-3) \leq 4`

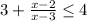
Adding -4 on both sides, we get,

`(x-2)/(x-3) -1 \leq 0`

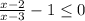
i.e.
`(x-2-x+3)/(x-3) \leq 0`

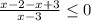
i.e.
`(1)/(x-3) \leq 0`

So, we have the inequality
`(1)/(x-3) \leq 0`.

Its critical points are given by x-3 = 0 which implies x = 3.

Now, we will find the region among the two
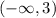`( - \infty , 3 )` and
`( 3 , \infty )` that satisfies the inequality
`(x-2)/(x-3) -1 \leq 0`

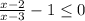
Substitute x = 2 in the above inequality, we get -1 < 0, which is true. Again, substitute x=4 gives 1 < 0, which is false.

As x=4 lie in the region
`( 3 , \infty )` , it cannot be the solution of the given inequality.

So, the solution of the given inequality is the region
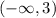`( - \infty , 3 )` .i.e. x < 3.

Hence. option A is correct.