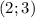Question

A system of equations is graphed on the coordinate plane. y=−x+5y=2x−1 What is the solution to the system of equations? Enter the coordinates of the solution in the boxes.

Answer 1

The coordinates of the solution is (2;3)

Answer 2

`(2;3)`

Explanation:

We can find the solution directly on the graph. The solution of a system of equations is the intersections between the two lines. Remember that each equation in this case represent a line, where the common points are always shown as an intersection.

To prove this result, we can apply other methods. Using the substitution method, we have to isolate one variable from one equation and then replace it in the other equation, like this:

`\left \{ {{y=-x+52'} \atop {y=2x-1}} \right.`

The variable y is already isolated, now we just replace the first equation in the second:

`-x+5=2x-1\\5+1-2x+x\\6=3x\\x=(6)/(3)=2`

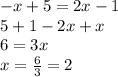
Then, we replace the x-value in one equation, no matter which one:

`y=2x-1\\y=2(2)-1\\y=4-1=3`

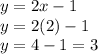
Therefore, we found that the solution is

`(2;3)`