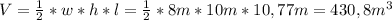Question

A right triangular prism is shown. Find (A) the total surface area and (B) the volume. You must show formulas and your work.

10m height
8m width
10.77m

Answer 1

Hello!

We are going to use the rectangular prism of the image as a guide:

First of all, the AC segment is calculated using the Pythagoras' theorem:


`AC= \sqrt{ AB^(2)+ BC^(2) } =\sqrt{ 10^(2)+ 8^(2) }=12,81 m`

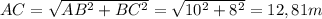
(A) The surface area of a prism is the sum of the surface areas of each face.

For the 2 triangles ABC and DEF


`A=2*(1/2*b*h)=2*(1/2*8m*10m)=80m`

For the ABEF Rectangle


`A=w*l=10,77m*10m=107,7m^(2)`

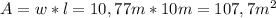
For the ACDE Rectangle


`A=w*l=10,77m*12,81m=137,96 m^(2)`

For the BCDF Rectangle


`A=w*l=10,77m*8m=86,16 m^(2)`

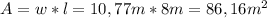
To finish you need to sum up the areas of each face:


`SA=2A_(ABC)+ A_(ABEF)+A_(ACDE)+A_(BCDF)= \\ 80 m^(2) +107,7m^(2) +137,96m^(2) +86,16m^(2) =411,82m^(2)`

(B) The volume of a prism is the product of the area of its base and the height of the prism. In this case, the base is a triangle so the formula and the calculations for the volume are as follows


`V= (1)/(2) *w*h*l= (1)/(2)* 8m*10m*10,77m=430,8m^(3)`