Question

Find the number of real number solutions for the equation. x2 – 18 = 0

cannot be determined

1

0

2

Answer 1

The number of real roots is 2.

Explanation:

Given,

`x^2 -18 = 0`

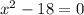
We will find the number of roots by Descartes' rule of signs.

Let,

`f(x)=x^2-18`

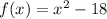
Since,

`f(x) = + x^2 - 18`

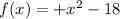
That is, the change in the sign shows, the given polynomial has one positive real root.

Now, by putting x = - x,

`f(-x)=(-x)^2- 18 = x^2 - 18`

`\implies f(-x) = + x^2 - 18`

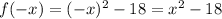
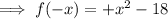
That is, the change in the sign shows, the given polynomial has one negative real root.

We know that, given polynomial has degree 2,

⇒ It only has 2 roots one is positive real and another is negative real,

⇒ f(x) having 2 real roots.

Answer 2

x ^ 2 - 18 = 0
For this case, the first thing you should do is rewrite the expression:
x ^ 2 - 18 = 0
x ^ 2 = 18
The solutions for this case are:
x1 = root (18)
x2 = -raiz (18)
Therefore the answer is:
2 solutions of real numbers.
Answer:
2