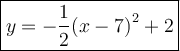1 Answer

Awais Jameel · Answer 1 · 2022-02-24T11:51:56+0000

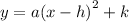
$y = a {(x - h)}^(2) + k$

where a-term determines the shape of graph.

h-term determines the change of graph for x-axis.

k-term determines the change of graph for y-axis.

Vertex of the graph is at (h,k).

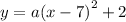
$y = a {(x - 7)}^(2) + 2$

We need to find the value of a-term. We have the given root which we can substitute in the equation.

Also the roots are on x-axis, meaning that the y-value for roots must be 0.

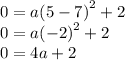
$0 =a {(5 - 7)}^(2) + 2 \\ 0 =a {( - 2)} ^(2) + 2 \\ 0 = 4a + 2$

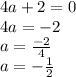
$4a + 2 = 0 \\ 4a = - 2 \\ a = ( - 2)/(4) \\ a = - (1)/(2)$

Therefore the value of a is - 1/2. Rewrite the equation as we get the answer.

$\large \boxed{y = - (1)/(2) {(x - 7)}^(2) + 2}$

Please log in or register to add a comment.