Question

Prove the divisibility of the following numbers:

51^7-51^6 by 25

Answer 1

Explanation:

`51^7-51^6=51^(6+1)-51^6\\\\\text{use}\ a^n\cdot a^m=a^(n+m)\\\\=51^6\cdot51^1-51^6\cdot1\\\\\text{use the distributive property}\ a(b-c)=ab-ac\\\\=51^6\cdot(51-1)=51^6\cdot50=51^6\cdot(2\cdot25)=25\cdot(51^6\cdot2)`

`\text{One of the factors of the product is the number 25.}\\\\\bold{CONCLUSION:}\\\\\text{The whole product is divisible by 25.}`

`\text{Therefore}\ 51^7-51^6\ \text{is divisible by 25.}`

Answer 2

To prove the divisibility lets expand each number first to get the complete picture of the problem

51^7 = 8.974106779 . 10^11

51^6 = 1.75962878 . 10^10

(51^7 - 51^6) = 8.974106779 . 10^11 - 1.75962878 . 10^10

= 8.798143901. 10^11

`(8.798143901. 10^11)/(25)`

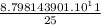
= 3.51925756. 10^10

That is the answer expressed in scientific notation

= 35192575600

Which means the divisibility is proven