Question

Jen Butler has been pricing speed pass train fares for a group trip to new york. three adult and four children must pay $122. two adults and three children must pay $87. find the price of the adult ticket and the price of the child

Answer 1

Let price of adult ticket is $x

And price of child ticket is $y

So we can make two equations using the given data

`3x+4y = 122`

`2x+3y = 87`

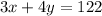
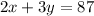
Now we can use eliminator method to solve the two equations

Multiply first equation by 2 and second equation by -3

`2(3x+4y = 122)`

`-3(2x+3y = 87)`

`6x+8y = 244`

`-6x-9y =-261`

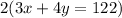
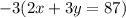
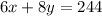
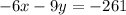
now add both the equations so we get

`6x-6x+8y-9y=244-261`

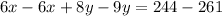
combine the like terms

`-y=-17`

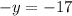
Divide both sides by -1

`y=17`

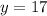
Plug y=17 in any one of the equations to solve for x

`3x+4(17) = 122`

`3x+68 = 122`

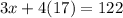
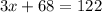
Subtract 68 from both sides

`3x = 54`

Divide both sides by 3

`x=18`

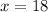
So x=18 and y=17

So

Price of adult ticket= $18

Price of child ticket = $17