Question

High statement is true? Y=log10^x is not a logarithmic function because the base is greater than 0

Answer 1

C.) y=log1X is not a logarithmic function because the base is equal to 1. XD
Just took the test!!

Sorry I didn't see this earlier

Answer 2

Option 3 -
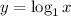`y=\log_(1)x` is not a logarithmic function because the base is equal to 1.

Explanation:

To find : Which statement is true?

Solution :

As the function defined in all statement is logarithmic function.

So, The definition of logarithmic function is defined as

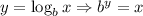`y=\log_bx\Rightarrow b^y=x` where, b>0 and b ≠ 1.

Now, The following statement

1)
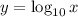`y=\log_(10)x` is not a logarithmic function because the base is greater than 0.

The statement is False as by definition, the base of a log must be greater than zero but cannot equal one.

2)
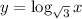`y=\log_(\sqrt3)x` is not a logarithmic function because the base is a square root.

The statement is False as by definition, the base
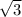`\sqrt3` is a positive number not equal to one.

3)
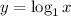`y=\log_(1)x` is not a logarithmic function because the base is equal to 1.

The statement is True as by definition log cannot have a base of one.

4)
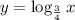`y=\log_{(3)/(4)}x` is not a logarithmic function because the base is a fraction.

The statement is False, as 3/4 is a legitimate base, just like any other positive number other than one.

Therefore, Option 3 is true.