Answer:
1. False.
2.False.
3.
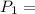 2
2
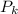 =2+4+6+.....+2n= n(n+1)
=2+4+6+.....+2n= n(n+1)
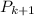 =2+4+6+....+2(k+1)=(k+1)(k+2)
=2+4+6+....+2(k+1)=(k+1)(k+2)
Explanation:
1.Given
4.6+5.7+6.8+.....+4n(4n+2)=
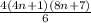
First , we prove for n=1
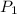 = 4.6=24
= 4.6=24
Left hand side :
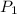 =
=
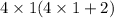
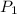 =24
=24
Right hand side:
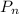 =
=
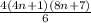
Put n=1
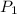 =
=
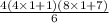
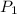 =
=
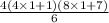
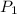 =
=
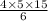
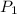 =50
=50
Hence, left hand side≠ right hand side
Therefore, the given statement is false.
2.
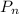 =12+42+72+.......(3n-2)2=
=12+42+72+.......(3n-2)2=
similarly , we prove that in the same manner
First , we prove for n=1 the given statement is true or false.
Take n=1
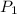 =12
=12
Left hand side :
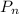 =(3n-2)2
=(3n-2)2
Put n=1 then
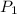 =
=
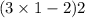
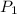 =2
=2
Right hand side:
) )/(2)](https://img.qammunity.org/2019/formulas/mathematics/high-school/wjzfh6zxrt77ydu910vnxcei7297ht9v4i.png)
Put n=1
Then we get
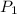 =
=
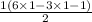
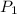 =
=
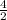
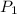 =2
=2
Hence , left hand side≠right hand side ≠
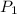
Therefore, the given statement is false.
3. Given that
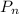 =2+4+6+....+2n=n(n+1)
=2+4+6+....+2n=n(n+1)
Put n= 1
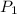 =2
=2
Put n=k then we get the statement Pk
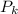 =2+4+6+....+2k=k(k+1)
=2+4+6+....+2k=k(k+1)
Now , Put n= k+1 and then we get the statment Pk+1
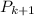 =2+4+6+....+2(k+1)=(k+1)(k+2).
=2+4+6+....+2(k+1)=(k+1)(k+2).