Question

Marianne wants to build a walkway around her rectangular garden. The width of her garden is one-third the length.

The perimeter of Marianne’s garden is 40 feet.

What is the length and width of her garden?

Answer 1

Write a system of equation based on the problem
⇒First equation depicts "the width of her garden is one-third the length"

`w= (1)/(3)l`

`w= \cfrac{l}{3}`
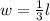
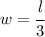
⇒Second equation depicts "the perimeter is 40 feet"
perimeter = 40
2l + 2w = 40
2(l + w) = 40
l + w = 40/2
l + w = 20

Solve the system of equation, substitute
`\cfrac{l}{3}` as w to the second equation to find the length
l + w = 20

`l+ (l)/(3)=20`

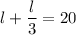
Equalize the denominators

`(3l)/(3)+ (l)/(3)=20`

`(3l)/(3)+ (l)/(3)=20`

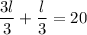
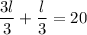
Simplify the numerators

`(4l)/(3) =20`
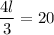
4l = 20 × 3
4l = 60
l = 60/4
l = 15
The length is 15 feet

Substitute the value of l to the first equation to find the width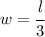

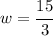
`w= \cfrac{l}{3}`

`w= \cfrac{15}{3}`
w = 5
The width is 5 feet