Question

This figure is made up of a rectangle and parallelogram.

What is the area of this figure?



Enter your answer in the box. Do not round any side lengths.

Answer 1

Area of Rectangle = 39
Total Area= 51
Length=3/13
Width= /13
Area of Parallelogram= 12

Answer 2

This figure is made up of a rectangle BDFE and parallelogram ABCD.

The area of this figure= Area of BDFE+Area of ABCD

Area of parallelogram=base*height and Are of rectangle= length*Width

So, Area of ABCD= CD*BH

And, Area of BDFE=BD*DF

area of this figure= BD*DF+CD*BH

From the figure CD=4 and BH=3

To find BD, Let us apply Pythagorean theorem,
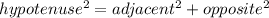`hypotenuse^(2) =adjacent^(2)+ opposite^(2)`, to ΔBHD

`BD^(2) =HD^(2)+ BH^(2)`

HD=2 and BH=3

`BD^(2) =2^(2)+ 3^(2)`

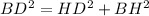
`BD^(2) =4+ 9=13`

`BD=√(13)`

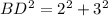
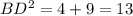
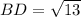
To find DF, Let us apply Pythagorean theorem,
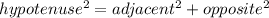`hypotenuse^(2) =adjacent^(2)+ opposite^(2)`, to ΔBHD

`DF^(2) =DG^(2)+ GF^(2)`

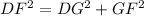
DG=6 and GF=9

`DF^(2) =6^(2)+ 9^(2)`

`DF^(2) =36+ 81=117`

`BD=√(117)=3√(13)`

`BD=√(13) and DF=3√(13)`

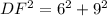
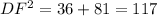
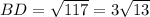
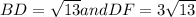
area of this figure= BD*DF+CD*BH

area of this figure=
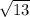`√(13)`*3
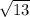`√(13)`+4*3

area of this figure=13*3+12

area of this figure=39+12=51

Area of this figure=51 square units