Question

Keith had 694 green, yellow and blue marbles altogether. he had 3 times as many blue marbles as yellow marbles. there were 90 fewer green than blue marbles. how many blue marbles did Keith have?

Answer 1

Let
`g` the number of green,
`y` the number of yellow and
`b` the number of blue marbles respectively.

We have


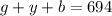
`g + y + b = 694` (we will call this equation 1)

Also,
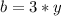
`b = 3*y` (yellow marbles are three times as many as blue marbles), so equation 1 becomes


`g + y + 3y = 694`

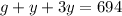
But,
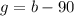
`g = b - 90` (green marbles are as many as blue marbles - 90)
and because
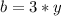
`b = 3*y`, we have that
`g = 3*y - 90`

So, equation 1 is now


`3y - 90 + y + 3y = 694`

`7y - 90 = 694`

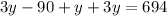
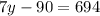
We add 90 to both sides so


`7y = 694 + 90 = 784`

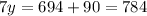
We divide each side by 7, so finally


`y = 112`

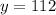
and we have


`b = 3*y = 3*112 = 336`
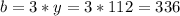
and

`g = b - 90 = 336 - 90 = 246`

To check if our results are correct, we can see that


`g + b + y = 246 + 336 + 112 = 694`,

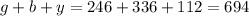
so we are indeed correct.

Answer 2

let the number of blue marbles be x

number of yellow marbles = x/3

number of green = x- 90

ATQ

x + x/3 + x - 90 = 694

2x + x/3 = 784

(6x + x)/3 = 784

7x/3 = 784

x = 784 x 3/7

x = 112 x 3

x = 336

number of blue marbles = 336