Answer:
Option A -
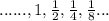
Explanation:
Given : A geometric has
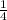 as its's fifth term and
as its's fifth term and
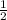 as common ratio.
as common ratio.
To find : Which sequence is geometric ?
Solution :
The geometric sequence is defined as
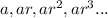
where, a is the first term and r is the common ratio.
The nth term of the sequence is
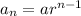
We have given,
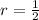 and
and
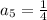
The 5'th term is
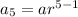
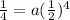
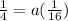
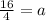
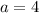
The sequence form is
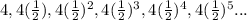
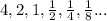
From the given sequence Option A matched with result.
Therefore, Option A is correct.