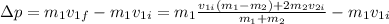Question

What is the change in momentum in a perfectly elastic collision of a ball that has a mass of 1kg and velocity of 12 m/s?

Answer 1

The exact value of the change in momentum depends on the mass and the initial velocity of the other body against which the ball collides. However, since it is an elastic collision, we can say that:
1) The total momentum of the two bodies is conserved after the collision
2) The total kinetic energy of the two bodies is conserved after the collision
This translates into the two following conditions:


`m_1 v_(1i) + m_2 v_(2i) = m_1 v_(1f) + m_2 v_(2f)`

`(1)/(2) m_1 v_(1i)^2 + (1)/(2) m_2 v_(2i)^2 = (1)/(2) m_1 v_(1f)^2 + (1)/(2) m_2 v_(2f)^2`
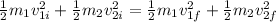
where the labels 1,2 refer to the two bodies, while i,f means 'initial' or 'final'.
Solving the two equations simultaneously we can find the final velocity of object 1 (the ball):

`v_(1f)= (v_(1i)(m_1-m_2)+2m_2 v_(2i))/(m_1+m_2)`
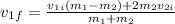
and therefore, its change in momentum will be

`\Delta p = m_1 v_(1f)-m_1 v_(1i)=m_1 (v_(1i)(m_1-m_2)+2m_2 v_(2i))/(m_1+m_2)-m_1 v_(1i)`