Answer:
D.
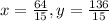
Explanation:
We have been given an image of two similar triangle. We are asked to find the values of x and y for our given triangles.
We will use Pythagoras theorem to solve for x and y.
In triangle ABC:
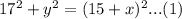
In triangle BCD:
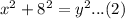
Upon substituting equation (1) in equation (1) we will get,






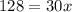
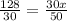
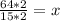
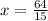
Upon substituting
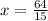 in equation (2) we will get,
in equation (2) we will get,
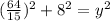
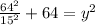
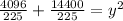

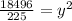
Taking square root of both sides we will get,
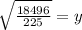
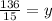
Therefore, the value of x is
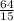 , value y is
, value y is
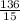 and option D is the correct choice.
and option D is the correct choice.