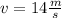Question

A baseball team is practicing throwing balls vertically upward to test their throwing arms. A player manages to throw a ball that reaches a maximum altitude of 10 m above the launch point, before falling back down. The acceleration due to gravity is 9.80 m/s 2 . (a) With what initial speed was the ball thrown?

Answer 1

We can solve this problem using the law of conservation of energy.
This law states that energy in a closed system must stay same.
That means that the energy of a ball leaving the hand and the energy of a ball when it reaches its maximum height must be the same.
The energy of a ball leaving the players hand is kinetic energy:

`E_k=(mv^2)/(2)`
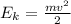
The energy when the ball reaches its maximum height ( and has zero velocity) is potential energy in a gravitational field:

`E_p=mgh`
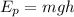
As said before these energies must be the same, and that allows us to find the initial speed:

`E_k=E_p\\ (mv^2)/(2)=mgh\\ v^2=2gh\\ v=√(2gh)`
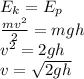
When we plug in all the number we get that
`v=14(m)/(s)`