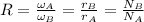Question

The equation for gear ratio

Answer 1

In a gear train with two gears, the gear ratio is defined as follows

`R= (\omega _A)/(\omega _B)`

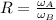
where
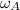
`\omega _A` is the angular velocity of the input gear while
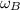
`\omega _B` is the angular velocity of the output gear.

This can be rewritten as a function of the number of teeth of the gears. In fact, the angular velocity of a gear is inversely proportional to the radius r of the gear:

`\omega = (v)/(r)`
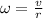
But the radius is proportional to the number of teeth N of the gear. Therefore we can rewrite the gear ratio also as

`R= (\omega _A)/(\omega _B) = (r_B)/(r_A) = (N_B)/(N_A)`