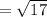Question

Given a triangle with vertices U(6, −1), W(0, −5), and X(4, −9), and Y is the midpoint of segment UW and Z is the midpoint of segment WX comma what is the length of YZ?

Answer 1

Be more specific. Like what is it asking you to do ? I'm trying to help. :)

Answer 2

Here we have to use the distance formula

Please see the image attached with the solution , for the figure

Firstly we have to find the length of line segment XU

and the triangle has a property that the length of line segment that connects the midpoint of the two sides is half the length of the third side.

It means here

Length of YZ = half the length of XU

So lets find the length of XU

`√((x_2-x_1)^2+(y_2-y_1)^2)= √((6-4)^2 +(-1+9)^2) =√(4+64)`

`=√(68)`

`=2√(17)`

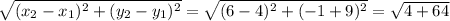
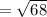
Now the length of YZ = half of
`=2√(17)`

So length of YZ =
`=√(17)`