The equation
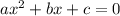
has solutions given by
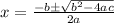
. This means take the numbers a, b and c then plug them into that formula on your calculator and bam, answers.
The
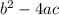
bit is called the discriminant and it tells you what kind of solutions occur,
-if
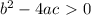
then the equation has two different solutions
-if

then the equation has exactly one solution
-if
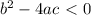
then the equation has no (real) solutions.
So you are interested in exactly one solution which happens if

or equivalently
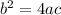
.