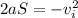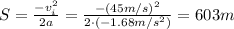Question

A driver in a 2144 kg car traveling at 15 m/s hits the brakes, coming to a stop in 67 meters. How far would it take the car to stop if it was instead traveling at 45 m/s?

Answer 1

1) First, let's calculate the value of deceleration a that the car can achieve, using the following relationship:

`2aS = v_f^2-v_i^2 = -v_i^2`
where S=67 m is the distance covered, vf=0 is the final velocity of the car, and vi=15 m/s is the initial velocity. From this we can find a:

`a= (-v_i^2)/(2S)= (-(15m/s)^2)/(2\cdot 67 m)=-1.68 m/s^2`

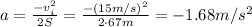
2) Then, we can assume this is the value of acceleration that the car is able to reach. In fact, the force the brakes are able to apply is

`F=ma`
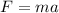
This force will be constant, and since m is always the same, then a is the same even in the second situation.

3) Therefore, in the second situation we have a=-1.68 m/s^2. However, the initial velocity is different: vi=45 m/s. Using the same formula of point 1), we can calculate the distance covered by the car before stopping:

`2aS=-v_i^2`

`S= (-v_i^2)/(2a) = (-(45 m/s)^2)/(2\cdot (-1.68 m/s^2))=603 m`