Question

What is the line of symmetry for the parabola whose equation is y = x2 + 10x + 25? x = -10 x = -5 x = 5

Answer 1

y = x2 + 10x + 25? x = -10 x = -5 x = 5

Answer 2

`y=x^2 + 10x + 25\\\\y=(x+5)^2`

Used the identity,
`(a+b)^2=a^2+2ab+b^2`

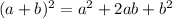
The given parabola is of the form ,
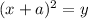`(x+a)^2=y`, having vertex at ,which can be obtained by

x+a=0

x= -a

(-a,0).

So, vertex of the given parabola is , at (-5,0).

The Meaning of term line of symmetry,is that line which divides the parabola in two equal halves.

Drawing the parabola,and finding the line of symmetry,which can be obtained by drawing a line parallel to y axis, passing through (-5,0).

So, the equation of line is : x= -5