Answer: 8.62 meters
Explanation:
Given: The height of the rock, in meters, is given by the function
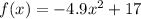 , where x is the number of seconds after Noelle releases her rock.
, where x is the number of seconds after Noelle releases her rock.
The height of Cesar’s rock, in meters, is given by the function
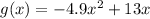 , where x is the number of seconds after he releases his rock.
, where x is the number of seconds after he releases his rock.
The moment when the rocks are at the same height then f(x)= g(x)
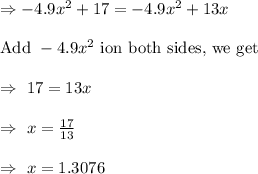
To calculate height put x in first equation, we get
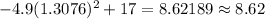
Hence, the height = 8.62 meters