Let x and y be the number of hours Ryan works on each job respectively. He can work no more that 10 hours a week, it means that the sum of x and y must be less than or equal to 10:
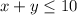
He also need to earn at least $72 a week, which means that the sum of 9 times x and 18 times y must be greater than or equal to 72:
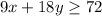
The system of inequalities is:
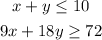
To graph these inequalities, we have to graph the boundary lines which are x+y=10 and 9x+18y=72, and then shade the region depending on the inequality. For the first inequality which is a less than or equal to, the shaded region must be under the boundary line (which is a continuous line) and for the second one, the shaded region must be above the boundary line (which is also continous).
In this case we only can take the solutions that have positive values of x and y, since Ryan can't work a negative number of hours. For example, one combination that will allow Ryan reach his goal is 5 hours as babysitter and 5 hours at the coffee shop.