Question

From a sample with nequals=1616​, the mean number of televisions per household is 22 with a standard deviation of 11 television. using​ chebychev's theorem, determine at least how many of the households have between 00 and 44 televisions.

Answer 1

Chebyshev's inequality:
For a wide class of distributions, no more than
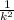
`(1)/(k^2)` of the values can be outside of k standard deviations of the mean.

Here,
n = 16
μ = 2
σ = 1
range iin question = 0 to 4
`=2\pm2=\mu\pm\sigma`
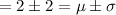
=> k=2

`(1)/(k^2)=(1)/(4)`
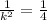
meaning that at most 1/4 of the sample is outside the given range, or 3/4 of the sample= (3/4)*16 =12 is within the given range of 0 to 4 televisions.

Answer: at least 12 out of 16 households have between 0 to 4 televisions, according to the Chebyshev's inequality.