Answer:
The sampling distribution of the sample proportion will be approximately normally distributed with mean
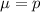 and standard deviation
and standard deviation
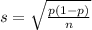
Explanation:
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
If np >= 15 and n(1-p) >= 15
Can be approximated to the normal distribution, with mean
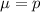 and standard deviation
and standard deviation
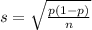
So
The sampling distribution of the sample proportion will be approximately normally distributed with mean
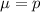 and standard deviation
and standard deviation