ive n
lan A
Plan B
Monday: 3 clients - Plan A
5 clients - Plan B
Total 10 hours
Tuesday
6 clients - Plan A
2 clients - Plan B
Total 10 hours
rocedure
Let's define a system of linear equations that represents the above problem.
A: Number of hours of workout in plan A
B: Number of hours of workout in plan B
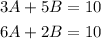
The goal here is to solve
3A+5B=10 and
6A+2B=10 for the variables A and B.
The solutions to your equations are:
A = 5/4 hour
B = 5/4 hour