Question

A group of engineers is building a parabolic satellite dish whose shape will be formed by rotating the curve y = ax2 about the y-axis. if the dish is to have a 10-ft diameter and a maximum depth of 3 ft, find the value of a and the surface area s of the dish. (round the surface area to two decimal places.)

Answer 1

`a=(3)/(25)`

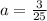
The Surface area of the dish is 62.83 ft²

Explanation:

Given : A parabolic satellite dish whose shape will be formed by rotating the curve
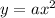`y=ax^2` about the y-axis.

The dish has a 10-ft diameter and a maximum depth of 3 ft,

We have to find the value of a and the surface area S of the dish.

Consider the parabolic satellite dish (shown below) formed by rotating the curve
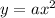`y=ax^2` about the y-axis.

Since the diameter is 10 ft

So radius is 5 ft and height is 3 ft.

So the coordinate A is (5, 3)

Also, (5, 3) satisfies the equation
`y=ax^2`

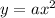
Thus,
`3=a(5)^2`

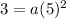
Simplify for a , we have,

`a=(3)/(25)`

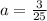
Thus, the Equation of curve is
`y=(3)/(25)x^2`

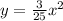
Now, we have to find the surface area of this figure formed by rotating the curve
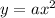`y=ax^2` about the y-axis.

Let R = x

Then Surface area is given by

`S=\int\limits^0_3 {2\pi x} \, dy`

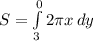
Finding value of x from
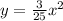`y=(3)/(25)x^2` we have,

`x=\sqrt{(25)/(3)y }`

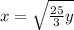
Thus,
`S=\int\limits^0_3 {2\pi\sqrt{(25)/(3)y } \, dy`

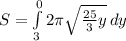
Simplify, we have,

`S=(10\pi)/(√(3)) \int\limits^0_3 {√(y) \, dy`

`S=(10\pi)/(√(3)) (2)/(3) y^{(3)/(2)} |_0^3`

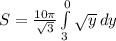
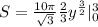
We get,

`S=(10\pi)/(√(3)) (2)/(3) (3)^{(3)/(2)}\\\\ S=(10\pi)/(√(3)) (2)/(3)\cdot 3√(3)\\\\ S=20\pi`

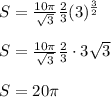
Simplify, We get,

S = 62.8318530718

Thus, The Surface area of the dish is 62.83 ft²

Answer 2

we have that
D=10 ft-------- > r= 5 ft
deep=3 ft
y=ax²
then
3=a*(5)²-------------- > a=3/25
y=(3/25)x²------------ > for x interval [0,5]

the answer part 1) is a=(3/25)

A differential of arc length is given by the Pythagorean theorem:
(ds)^2 = (dx)^2 +(dy)^2
then
ds = √(1 +(dy/dx)^2)·dx
dy/dx = (3/25)*(2x)=(6x/25)

Remember that when you revolve an arc around some axis, you multiply this value by the radius to get the surface area of revolution.

therefore

The dish area (A) is given by the integral
A = ∫[0, 5] 2π·x·√(1 +(dy/dx)^2)·dx
where dy/dx = (6x/25)
A = 2π/25·∫[0, 5] x√(625 +36x^2)·dx
∫x√(a +bx^2)·dx = (a +bx^2)^(3/2)/(3b)
.. = 2π/25·(625 +36x^2)^(3/2)/(3*36) |[0, 5]
.. = (π/1350)*[(625 +36*25)^(3/2) -625^(3/2)]
.. = 102.2254 ft²----------------- > 102.23 ft²

the answer part 2) is 102.23 ft²