Question

For f(x)=4x+1 and g(x)=x^2-5 find (fog)(x)

Answer 1

(fog)(x)= f(g(x))= 4(x^2-5)+1= (4•x^2)-20+1=

(4•x^2)-19

Answer 2

(fog)(x) =
`4x^(2)-19`

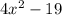
Explanation:

The given functions are f(x) = 4x + 1 and g(x) =
`x^(2)-5`

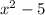
We have to find the value of (fog)(x).

Since (fog)(x) = f[g(x)]

It means we have to find the value of f(x) for the value of x = g(x)

Now f[g(x)] =
`4[x^(2)-5]+1`

=
`4x^(2)-20+1`

=
`4x^(2)-19`

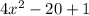
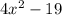
Therefore, f[g(x)] =
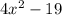`4x^(2)-19` will be the answer.