Question

Find the zeros and state whether the multiplicity of each zero is even or odd. What are the zeros of​ f?

Answer 1

A zero of a function f is where f(x) is equal to zero. You can see that the y-coordinate is zero in two places: for x = -1 and for x =1.

The multiplicity of a root is the number of times it appears as a factor in the function. For example, in
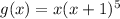
`g(x) = x(x+1)^5`, -1 has a multiplicity of five, and 0 has a multiplicity of one. If the multiplicity is an even number, then the graph touches zero and then rebounds (it does not change sign). This is because raising a number to an even power maintains its sign. If the multiplicity is odd, then the graph touches zero and cross the x-axis, changing its sign.

Here, -1 has an odd multiplicity, and 1 has an even multiplicity.

This could be the equation of
`f(x) = (x-1)^2(x+1)`.