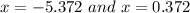Question

If the quadratic formula is used to solve 2x(x + 5) = 4, what are the solutions? {-1/2, -9/2}

Answer 1

x²+bx=c
x=[-b+√(b²+4c)]/2

2x(x+5)=4
2x²+10x=4
x²+5x=2

x=[-5+√(5²+4*4)]/2

if b=-1/2 and c=-9/2
x= {1/2+√[(1/2)²+4*(-9/2)]}/2

Answer 2

The solutions are:

`x=-5.372\ and\ x=0.372`

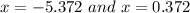
Explanation:

The equation is given by:

`2x(x+5)=4`

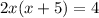
on using the distributive property of multiplication in the left hand side of the equation we have:

`2x* x+2x* 5=4\\\\i.e.\\\\2x^2+10x=4\\\\i.e.\\\\2x^2+10x-4=0\\\\i.e.\\\\2(x^2+5x-2)=0\\\\i.e.\\\\x^2+5x-2=0`

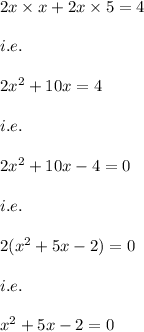
Now, we know that the solution of the quadratic equation:

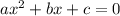`ax^2+bx+c=0` is given by:

`x=(-b\pm √(b^2-4ac))/(2a)`

Here we have:

`a=1,\ b=5\ and\ c=-2`

Hence, the solution is:

`x=(-5\pm √(5^2-4* 1* (-2)))/(2* 1)\\\\i.e.\\\\x=(-5\pm √(25+8))/(2)\\\\i.e.\\\\x=(-5\pm √(33))/(2)\\\\x=(-5+√(33))/(2),\ x=(-5-√(33))/(2)`

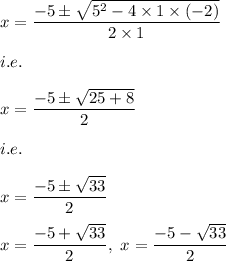
Hence, in decimal for the solution is:

`x=-5.372\ and\ x=0.372`