The area is equal to length times width.

The perimeter is equal to twice the sum of the length and the width.
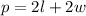
We know that the perimeter is 450 meters, the length is

meters, and the width is

meters.
To maximize the area, we find the global maximum of the function
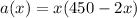
. The easiest way is to use the formula for the vertex,
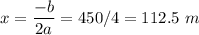
, and
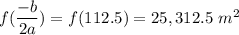
.
I realize it sounds like a big number, but the largest area that can be enclosed is 25,312.5 m^2 (if I did this correctly!).