Answer:
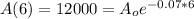
And solving for the initial amount
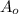 we got:
we got:
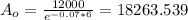
So then the original price for the car would be approximately 18263.539$
Explanation:
For this case we can use the exponential model given by:
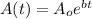
Where:
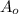 represent the initial amount for the car
represent the initial amount for the car
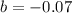 represent the exponential growth/decay rate
represent the exponential growth/decay rate
t represent the number of years. With t =0 at the begin
After 6 year we have that t =6, and we know this condition:
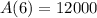
So then we can use the exponential model formula and the condition given and we have this:
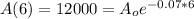
And solving for the initial amount
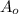 we got:
we got:
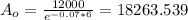
So then the original price for the car would be approximately 18263.539$