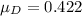We can solve the problem by analyzing the forces acting along the direction of the inclined plane. There are two forces: the first one is the component of the weight parallel to the inclined plane, which is

where

and
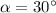
. This force points along the direction of the motion (down). The second one is the frictional force, acting against the motion, as well along the inclined plane:
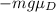
where
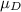
is the dynamic frictional coefficient, and we have to find the value of this. The negative sign means the force is acting against the direction of the motion.
Newton's second law states that the resultant of the forces acting on the object is equal to the product between the mass m and the acceleration a:
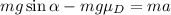
So we can write the acceleration as
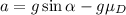
Now, we can use the law of motion along the direction of the inclined plane. For an uniformly accelerated motion, we have
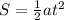
Assuming the object is initially at rest. But S, in our problem, is exactly the lenght of the plane:
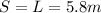
So we can substitute a inside the formula and we get
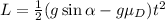
From which we get
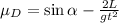
and using the time given by the problem,
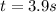
and
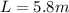
, we find