Question

Find the inverse of f(x)= x^3+10

g(x)=___

Answer 1

The inverse of a function undoes the operations of the original function.

In words, f(x) takes an input, x, raises it to the third power, and adds ten. The inverse takes an input x, raises it to the one-third power (cube root), and subtracts ten.

You find an inverse by interchanging x and y in an equation.


`f(x)= x^3+10 \\ y=x^3+10`


`x=y^3+10`

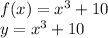
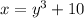
This is an inverse, but you want to find y in terms of x now.


`x-10=y^3`


`y=\sqrt[3]{x-10}`


`f^(-1) = \sqrt[3]{x-10}`

(Read: f inverse of x is the cube root of x minus ten).


`g(x) = \sqrt[3]{x-10}`

You can check your inverse by taking the composition of the function, or
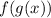
`f(g(x))`. If the result is x, then this is a valid inverse.


`f(g(x)) = ( \sqrt[3]{x-10})^3 + 10 = x-10+10 = x`

And that checks out, so we're done.