Question

If the hypotenuse of a 45-45-90 triangle is 13, what is the length of the legs?

Answer 1

The legs of this triangle are each of length 1 unit as they are both original sides of the unit square. That is, the legs of this 45-45-90 triangle are equal. Applying the Pythagorean theorem we find that the length of the hypotenuse is equal to the square root of 2.

Answer 2

In a 45-45-90 triangle, the length of the hypotenuse is
`√(2)` times the length of leg.

As per the statement:

If the hypotenuse of a 45-45-90 triangle is 13 units.

To find the length of the legs.

Using above definition:

`\text{Length of Hypotenuse} = √(2) * \text{Length of the leg}`

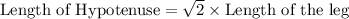
Substitute the given values we have;

`13 = √(2)  * \text{Length of the legs}`

Divide both sides by
`√(2)` we have;

`\text{Length of the legs} =[tex](13)/(√(2)) = (13√(2))/(2)`[/tex] units

Therefore, the length of the legs is
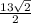`(13√(2))/(2)`[/tex] units