Question

Find two positive real numbers who's product is a maximum and whose sum is 156.

Answer 1

Let the two positive real numbers be x and y.
The sum of two numbers is 156, so we can write:

x+ y = 156
or
y = 156 - x

The product of two numbers = xy
Using the value of y in previous equation we can write:

Product = x(156 - x) = - x² + 156x

The above equation is a quadratic equation and results in a parabola. The maximum value of parabola with negative coefficient of x² lies at its vertex.

The x component of vertex will be =
`(-b)/(2a)`
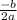
Here b is the coefficient of x term, and a is the coefficient of x² term.
So,
a = -1
b = 156
Using the values in the formula we get the x component of vertex x =
`(-156)/(-2)=78`

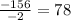
So x = 78
and

y = 156 - x = 156 - 78 = 78

Thus, the two numbers whose sum is 156 and which result in maximum product are 78, 78