Question

Find the distance between the two points. Round to the nearest tenth if necessary. (10, –4), (5, 8)

169

7

13

16

Answer 1

`d= √((10-5)^2+(-4-8)^2)= √(25+144)= √(169)=13`

Answer 2

Answer: 13

If you ask this question may be you do not know the formula of the distance between two points or you do not know how to use it, so I am going to explain you both.

1) Formula of the distance betweer two points:

Say the point A has coordinates (x1, y1) and the point B has coordinates (x2, y2), the distance, d, between the points A and B is given by the formula:


`d^2= (x_1-x_2)^2+(y_1+y_2)^2} = d=√((x_1-x_2)^2+(y_1-y_2)^2)`

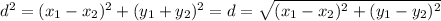
2) So, to apply that formula you need the coordinates of the two points.

In this case the coordinates of the point (10,-4) are: x = 10, y = -4

The coordinates of the point (5,8) are: x = 5, y = 8.

3) This is the application:


`d= √((10-5)^2+(-4-8)^2)= √((5)^2+(-12)^2)= √(25+144) d= √(169)=13`

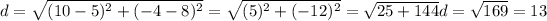
So, the answer is 13.