The equation of a circle is
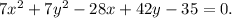
First divide the equation by 7 and group terms with x and with y:

In both brackets write a perfect square:
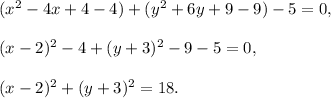
The equation of this circle in standard form is
 The center of the circle is at point (2,-3) and the radius is
The center of the circle is at point (2,-3) and the radius is
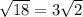 units.
units.