Answer:
C 28
Explanation:
Let:
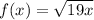
Now, let's evaluate every value, so we can determinate if the expression can be further simplified:
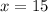
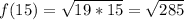
This can't be simplified because it can't be expressed as the product of a series of prime factors raised to the exponent of the root.
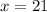
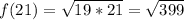
This can't be simplified because it can't be expressed as the product of a series of prime factors raised to the exponent of the root.
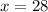
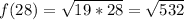
This can be simplified because you can rewrite the expression as:


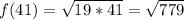
This can't be simplified because it can't be expressed as the product of a series of prime factors raised to the exponent of the root.