Question

Samantha took out two loans totaling $6,000 to pay her first year of college. She borrowed the maximum amount she could at 3.5% simple annual interest and the remainder at 7% simple annual interest. At the end of the first year, she owed $259 in interest. How much was borrowed at each rate?

Answer 1

Our simple interest formula is I = prt, where I is the amount of interest, p is the amount of principal, r is the percentage written as a decimal, and t is the amount of time (in this case in years). We will define our variable x as the amount borrowed at the lower percentage rate. Our formula would then look like

`I=x(0.035)(1) \\ =0.035x`. (Remember that when we convert percentages to decimals, we divide by 100; 3.5/100 = 0.035.)
The remaining money borrowed was invested at 7% interest. The expression to represent the remaining money would be 6000 - x, as it is what was left over to borrow. The interest formula for this loan would be

`I=(6000-x)(0.07)(1)`. (Again, we must divide 7 by 100 to convert the percentage; 7/100=0.07.)
Using the distributive property we have:

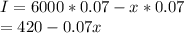
`I=6000*0.07-x*0.07 \\ =420-0.07x` (t in this case is 1, since it is 1 year.)
The total amount of interest for both loans for one year was $259, so we have:

`259=0.035x+420-0.07x`
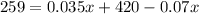
Combine our like terms:

`259=-0.035x+420`
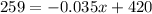
Cancel 420 by subtracting:

`259-420=-0.035x+420-420 \\ -161=-0.035x`
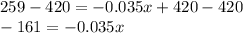
Cancel -0.035 by dividing:

`(-161)/(-0.035)=(-0.035x)/(-0.035) \\ 4600=x`
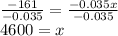
This means she borrowed $4600 at the lower interest rate. The remainder would be $6000-$4600=$1400 at the higher interest rate.