Question

PLEASE PLEASE PLEASE HELP. I have this class really soon.

You deposit $9000 into a bank account that pays 1 46% annual interest compounded daily How much interest does the account earn after 3 years?

Answer 1

This can be solved with the equation

`A=P(1+(r)/(n) )^(nt)`
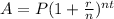
where A is the new/resulting balance

insert your interest r=0.0146
the starting amount P=9000
the number of times it gets compounded per year n=365 (every day)
and the number of years t=3

insert everything and calculate the balance in 3 years:

`A=9000(1+(0.0146)/(365) )^(365*3) \\ =9000(1.00004)^(365*3) \\ =9000*1.0447...\\ =9402.95`


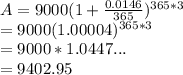
the amount earned over 3 years is then the new balance- the current balance:
9402.95-9000=402.95$ earned over 3 years

Answer 2

interest is compounded quarterly. SOLUTION. i think i relly just looked it up srry if it isn't right