Question

In the figure, WY¯¯¯¯¯¯¯¯¯WY¯ and XZ¯¯¯¯¯¯¯¯XZ¯ intersect at point VV, the measure of ∠WVZ∠WVZ is (11x−19)°(11x−19)°, and the measure of ∠WVX∠WVX is (8x+28)°(8x+28)°.

What is the measure of ∠YVZ∠YVZ?

Answer 1

Assuming a diagram similar to the one I've attached, ∠YVZ is a vertical angle to ∠WVX, which means they have an equal measure. Additionally, ∠WVZ and ∠WVX form a linear pair, which means they are supplementary (sum to 180°). That means we start out with the equation

`(11x-19)+(8x+28)=180`
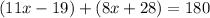
We combine our like terms (the x's get combined, then the constants get combined) and have:

`19x+9=180`
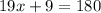
Cancel the 9 first by subtraction:

`19x+9-9=180-9 \\ 19x=171`
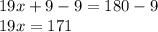
Cancel the 19 by division:

`(19x)/(19)= (171)/(19) \\ x=9`
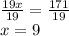
Since we know that our angle we're looking for, ∠YVZ, is the same measure as ∠WVX, we substitute 9 in for x:
8(9)+28=72+28=100°