Question

Use a system of equations to solve this problem. Hunter needs 10 oz of a snack mix that is made up of seeds and dried fruit. The seeds cost $1.50 per ounce and the dried fruit costs $2.50 per ounce. The 10 oz snack mix costs $2.20 per ounce. Let x = the amount of seeds. Let y = the amount of dried fruit. How much of each snack should Hunter purchase to satisfy the scenario? Enter your answers in the boxes.

Answer 1

The correct answer is 3 ounces of the seed and 7 ounces of the dried fruit.

Answer 2

The hunter should purchase 3 ounces of seeds and 7 ounces of dried fruit to satisfy the scenario.

Step-by-step explanation

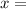`x=` the amount of seeds and
`y=` the amount of dried fruit.

As the hunter needs total 10 ounces of a snack mix , so the first equation will be..

`x+y= 10 .....................................(1)`

Now the seeds cost $1.50 per ounce and the dried fruit costs $2.50 per ounce. And the mixture costs $2.20 per ounce, so the second equation will be:

`1.50x+2.50y= 2.20*10\\ \\ 1.50x+2.50y= 22.........................................(2)`

According to the substitution method, we will isolate y from the first equation as
`y= 10- x`

Now we will substitute this
`y= 10- x` into the second equation in place of
`y`

`1.50x+2.50(10-x)= 22\\ \\ 1.50x+25-2.50x =22 \\ \\ -1.00x = 22-25 \\ \\ -1.00x= -3\\ \\ x= 3`

Plugging this
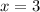`x=3` into the equation
`y= 10- x` , we will get...

`y= 10-3 =7`

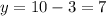
So, the hunter should purchase 3 ounces of seeds and 7 ounces of dried fruit to satisfy the scenario.