Question

When purchasing bulk orders of​ batteries, a toy manufacturer uses this acceptance sampling​ plan: randomly select and test 5858 batteries and determine whether each is within specifications. the entire shipment is accepted if at most 22 batteries do not meet specifications. a shipment contains 70007000 ​batteries, and 11​% of them do not meet specifications. what is the probability that this whole shipment will be​ accepted? will almost all such shipments be​ accepted, or will many be​ rejected?

Answer 1

We use the binomial distribution:

`P _(a)= \sum^c_d_=_0 (n!)/(d!(n-d)!) p^d (1-p)^n^-^d`
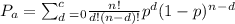
In this formula, c is the acceptable number of defectives; n is the sample size; p is the fraction of defectives in the population. Our c is 2; n is 58; and p is 0.11. Once we evaluate that summation, we get 0.0388. This has a 3.88% chance of being accepted. Since this is such a low chance, we can expect many of the shipments like this to be rejected.