Question

If it take 3.4 years for a radioactive isotope to decay to 1/16 of its initial value, what is the value of k for the isotope?

Answer 1

In this question, k stands for the decay constant. The half-life and decay constant of a radioactive isotope are related by the following equation:

Half Life = ln(2) / Decay Constant
ln(2) is the natural log of 2.

We are provided that in 3.4 years the isotope decays to 1/16 of its initial value.

`(1)/(16)= (1)/( 2^(4) )`
This means, in 3.4 years 4 half lifes are passed.

So, 4 Half lifes = 3.4 years
Half Life = 3.4/4 = 0.85 years.

Now we can find k by plugging in values in above equation:


`k= (ln(2))/(0.85)= 0.815`

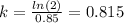
So the value of k for the isotope is 0.815 per year.