Question

Figure ABCD is rotated 90°counterclockwise about the origin. Which of the following gives the correct measure of an image of one of its sides?

B'C' = √17
C'D' = √10
D'D' = 5
A'B' = √17

Answer 1

its your last option or A'B'=17

Answer 2

The correct option is 4.

Explanation:

90°counterclockwise about the origin is a rigid transformation. It means the measure of corresponding sides of image and preimage are same.

`AB=A'B',BC=B'C',CD=C'D',AD=A'D'`

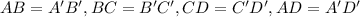
Distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

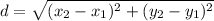
The measure of all sides are

`AB=A'B'=√((4-0)^2+(-3+4)^2)=√(17)`

`BC=B'C'=√((5-4)^2+(-6+3)^2)=√(10)`

`CD=C'D'=√((1-5)^2+(-7+6)^2)=√(17)`

`AD=A'D'=√((1-0)^2+(-7+4)^2)=√(10)`

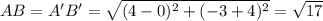
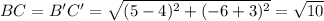
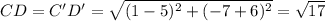
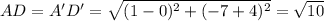
Since A'B' = √17 gives the correct measure of an image of one of its sides, therefore correct option is 4.