Question

In a recent​ year, an author wrote 169 checks. Use the Poisson distribution to find the probability​ that, on a randomly selected​ day, he wrote at least one check.

Answer 1

We should first calculate the average number of checks he wrote per day. To do that, divide 169 by 365 (the number of days in a year) and you get (rounded) 0.463. This will be λ in our Poisson distribution. Our formula is

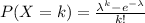
`P(X=k)= ( \lambda ^(k)-e^(-\lambda) )/(k!)`. We want to evaluate this formula for X≥1, so first we must evaluate our case at k=0.

`P(X=0)= (0.463 ^(0)-e ^(-0.463) )/(0!) \\ = (1-e ^(-0.463) )/(1) =0.3706`
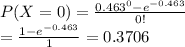
To find P(X≥1), we find 1-P(X<1). Since the author cannot write a negative number of checks, this means we are finding 1-P(X=0). Therefore we have 1-0.3706=0.6294.
There is a 63% chance that the author will write a check on any given day in the year.